“MNIST For ML Beginner”を動かしてみた

Date:2017.11.24

たかはし

今回はTensorFlowの公式チュートリアルである“MNIST For ML Beginner”を使って手書き数字を認識させたいと思います。また、おまけにTensorFlowの強力な可視化ツールであるTensorBoardも実装してみます。

TensorFlowのインストールは公式サイトを参考にしてください。

CPU版の場合は

$ pip install tensorflow

1	$ pip install tensorflow

GPU版の場合は

$ pip install tensorflow-gpu

1	$ pip install tensorflow-gpu

というコマンドでインストールできます。

私はAnacondaを利用してインストールしたので、こちらのサイトを参考にさせていただきました

“MNIST For ML Beginner”のコード解説

この章では、”MNIST For ML Beginner”のコードを前回の記事に沿って簡単に解説していきたいと思います。

このチュートリアルでは以下のようにモデルを学習させています。

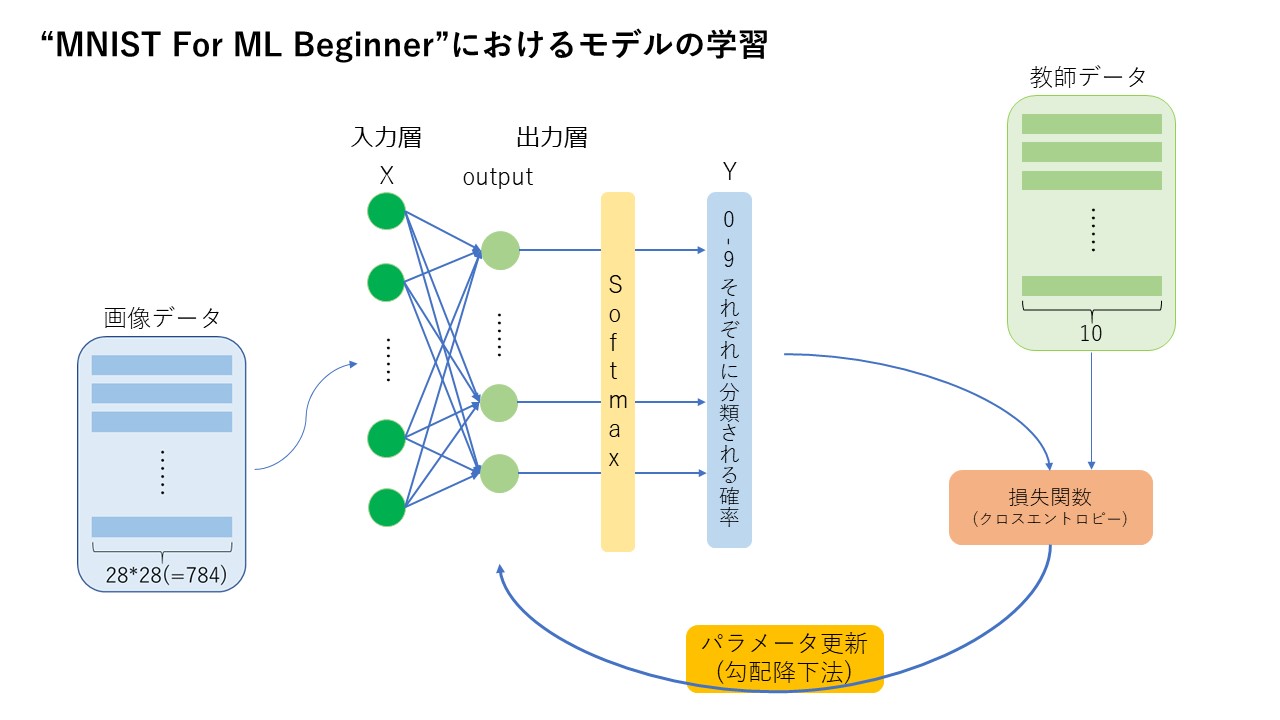
入力データとして階調8bit大きさ28×28のモノクロ画像を一次元配列にした画像データ(MNIST)を読み込み、入力層から出力層に順伝播を行った後、Softmax関数によって0-9の数字それぞれに分類される確率を出力します。この過程を少し詳しく見てみると、
入力データ

$X = \left( \begin{array}{cccc} x_1^{(1)} & x_2^{(1)} & \ldots & x_{784}^{(1)} \\ x_1^{(2)} & x_2^{(2)} & \ldots & x_{784}^{(2)} \\ \vdots & \vdots & \ddots & \vdots \\ x_1^{(N)} & x_2^{(N)} & \ldots & x_{784}^{(N)} \end{array} \right)$

に対して、重みとバイアスを

$W = \left( \begin{array}{cccc} w_{1,1} & w_{1,2} & \ldots & w_{1,10} \\ w_{2,1} & w_{2,2} & \ldots & w_{2,10} \\ \vdots & \vdots & \ddots & \vdots \\ w_{784,1} & w_{784,2} & \ldots & w_{784,10} \end{array} \right)$

$\bm{b} = \left( \begin{array}{c} b_1 \\ b_2 \\ \vdots \\ b_{10} \end{array} \right)$

と置くと、順伝播によって

$output = \left( \begin{array}{cccc} o_1^{(1)} & o_2^{(1)} & \ldots & o_{10}^{(1)} \\ o_1^{(2)} & o_2^{(2)} & \ldots & o_{10}^{(2)} \\ \vdots & \vdots & \ddots & \vdots \\ o_1^{(N)} & o_2^{(N)} & \ldots & o_{10}^{(N)} \end{array} \right) = X W + b$

が出力され、これに対してSoftmax関数を適用することで

$Y = \left( \begin{array}{cccc} p_0^{(1)} & p_1^{(1)} & \ldots & p_{9}^{(1)} \\ p_0^{(2)} & p_1^{(2)} & \ldots & p_{9}^{(2)} \\ \vdots & \vdots & \ddots & \vdots \\ p_0^{(N)} & p_1^{(N)} & \ldots & p_{9}^{(N)} \end{array} \right)$

( $p_i^{(n)}$ はn番目の入力データがiに分類される確率を表す)
のようにYが0-9それぞれの数字に分類される確率として出力されています

なおソフトマックス関数の出力はどの成分も0-1の値をとりその和は1となるので確率分布と読みかえることができ、それをここでは利用しています。

このモデルは入力された画像を0-9の数字に分類する多クラス分類のモデルであり、0-9の数字それぞれに分類される確率が出力されるので、損失関数としてクロスエントロピーを使用しています。

また今回は画像データのうち59,999コを学習用データ9,999コをテスト用データとし、訓練データでモデルを学習させたのちテストデータで精度を測定します。

では、以下で実際のコードを解説していきます。

はじめにTensorFlowのimportとデータの読み込みを行います。

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

import tensorflow as tf

from tensorflow.examples.tutorials.mnist import input_data

mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

次に入力データと教師データを格納するプレースホルダーを準備します。

引数shapeの要素をNoneとすれば可変長となり、後にミニバッチ(後述)の数を変える際やテストデータを入れる際に困りません。

x = tf.placeholder(tf.float32, [None, 784])
y_ = tf.placeholder(tf.float32, [None, 10])

1 2	x = tf.placeholder(tf.float32, [None, 784]) y_ = tf.placeholder(tf.float32, [None, 10])

最適化すべき変数も定義しておきます。なお今回は変数の初期値を0としています。

W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))

1 2	W = tf.Variable(tf.zeros([784, 10])) b = tf.Variable(tf.zeros([10]))

先ほどのY=softmax(XW+b)を計算します。

y = tf.nn.softmax(tf.matmul(x, W) + b)

1	y = tf.nn.softmax(tf.matmul(x, W) + b)

損失関数として出力と教師データのクロスエントロピーを定義します。

cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]))

1	cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]))

学習率を0.5として、勾配降下法も定義しています。

train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)

1	train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)

ここまででモデルの定義は終わったので、実際に学習を開始します。

TensorFlowではグラフ構造を定義した後、Sessionを呼び出してグラフ演算を行うという流れでテンソル計算を行います。データからランダムに100コずつミニバッチをとって学習していくことで計算量の削減及び局所解への収束の防止を図っています。

sess = tf.InteractiveSession()
#変数の初期化
tf.global_variables_initializer().run()
#学習の開始
for _ in range(1000):
   batch_xs, batch_ys = mnist.train.next_batch(100)
   sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})
   #feed_dictで実際にプレースホルダーにデータを入れ込んでいます

sess = tf.InteractiveSession()

#変数の初期化

tf.global_variables_initializer().run()

#学習の開始

for _ in range(1000):

batch_xs, batch_ys = mnist.train.next_batch(100)

sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})

#feed_dictで実際にプレースホルダーにデータを入れ込んでいます

モデルの学習が終了したら、精度として分類の正解率を測ります。

tf.argmaxは最大の成分のインデックスを返すので、確率が最大のインデックスと正解のインデックスが一致しているかどうかを測っています。

correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
#テストデータを入れて精度を測定
print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))

correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))

accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

#テストデータを入れて精度を測定

print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))

実行すると、91%の正解率でテストデータを認識できました。

実際に自分の書いた数字で試してみた

では、実際に自分の書いた数字を正しく予測できるか試してみたいと思います。

このような手書き数字を用意しました。

これを先ほどのモデルで予測させてみると、、、

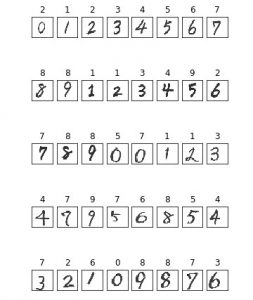
予測の正解率は65%でした。(画像の上に付いているのが予測として出力された数字です)

精度が大幅に下がってしまったのは、MNISTデータと文字の太さが異なることや少し崩れた文字を書いたことが原因と考えられます。今回は隠れ層の無い非常に簡単なモデルだったため、このようなデータの予測は上手くいきませんでしたが、ニューラルネットワークの多層化やCNNの導入などで精度は上がっていくと思います。

TensorBoardも実装してみた

さらに先ほどのコードにTensorBoardによる可視化を組み込んでみました(TensorBoardはTensorFlowにあらかじめ組み込まれているので、以下のようにコードを加えるだけで実装できます)。

ざっくり解説すると、通常通りTensorFlowグラフを作成(ただしノードの名前を指定及びname scopeでグループ化しておくと良い)→サマリーデータの記録→TensorBoardで可視化　という流れになっています。

#サマリーデータをTensorFlowイベントファイルとして保存するディレクトリを指定
log_dir = "path/to/log-directory"

import os
if not os.path.exists(log_dir):
   os.mkdir(log_dir)

#以下tf.name_scopeでグループ化していきます
with tf.name_scope("Input"):
   x = tf.placeholder(tf.float32, [None, 784])
   y_ = tf.placeholder(tf.float32, [None, 10])

with tf.name_scope("Variables"):
   W = tf.Variable(tf.zeros([784, 10]),name="Weight")
   b = tf.Variable(tf.zeros([10]),name="Bias")

with tf.name_scope("Layer1"):
   y = tf.nn.softmax(tf.matmul(x, W) + b,name="Softmax")

with tf.name_scope("Loss"):
   cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]),name="CrossEntropy")
   #ヒストグラムを作成します
   tf.summary.histogram("Histogram_CrossEntropy",tf.squeeze(cross_entropy))

#サマリーデータをまとめます    
summary_op = tf.summary.merge_all()

with tf.name_scope("TrainStep"):
   train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)

sess = tf.InteractiveSession()
tf.global_variables_initializer().run()

#サマリーデータを記録する為のインスタンスを作成します
summary_writer = tf.summary.FileWriter(log_dir, graph=sess.graph)

for i in range(1000):
   batch_xs, batch_ys = mnist.train.next_batch(100)
   sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})
   _,summary = sess.run([train_step,summary_op], feed_dict={x: batch_xs, y_: batch_ys})
   #随時サマリーデータを記録していきます
   summary_writer.add_summary(summary, i)
with tf.name_scope("Accuracy"):
   correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))
   accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32),name="Accuracy")
print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))

#サマリーデータをTensorFlowイベントファイルとして保存するディレクトリを指定

log_dir = "path/to/log-directory"

import os

if not os.path.exists(log_dir):

os.mkdir(log_dir)

#以下tf.name_scopeでグループ化していきます

with tf.name_scope("Input"):

x = tf.placeholder(tf.float32, [None, 784])

y_ = tf.placeholder(tf.float32, [None, 10])

with tf.name_scope("Variables"):

W = tf.Variable(tf.zeros([784, 10]),name="Weight")

b = tf.Variable(tf.zeros([10]),name="Bias")

with tf.name_scope("Layer1"):

y = tf.nn.softmax(tf.matmul(x, W) + b,name="Softmax")

with tf.name_scope("Loss"):

cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]),name="CrossEntropy")

#ヒストグラムを作成します

tf.summary.histogram("Histogram_CrossEntropy",tf.squeeze(cross_entropy))

#サマリーデータをまとめます

summary_op = tf.summary.merge_all()

with tf.name_scope("TrainStep"):

train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)

sess = tf.InteractiveSession()

tf.global_variables_initializer().run()

#サマリーデータを記録する為のインスタンスを作成します

summary_writer = tf.summary.FileWriter(log_dir, graph=sess.graph)

for i in range(1000):

batch_xs, batch_ys = mnist.train.next_batch(100)

sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})

_,summary = sess.run([train_step,summary_op], feed_dict={x: batch_xs, y_: batch_ys})

#随時サマリーデータを記録していきます

summary_writer.add_summary(summary, i)

with tf.name_scope("Accuracy"):

correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))

accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32),name="Accuracy")

print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))

そして、以下をコマンドすると

$ tensorboard --logdir="path/to/log_directory"

1	$ tensorboard --logdir="path/to/log_directory"

TensorBoardが起動するので、http://localhost:6006にアクセスすると、、、

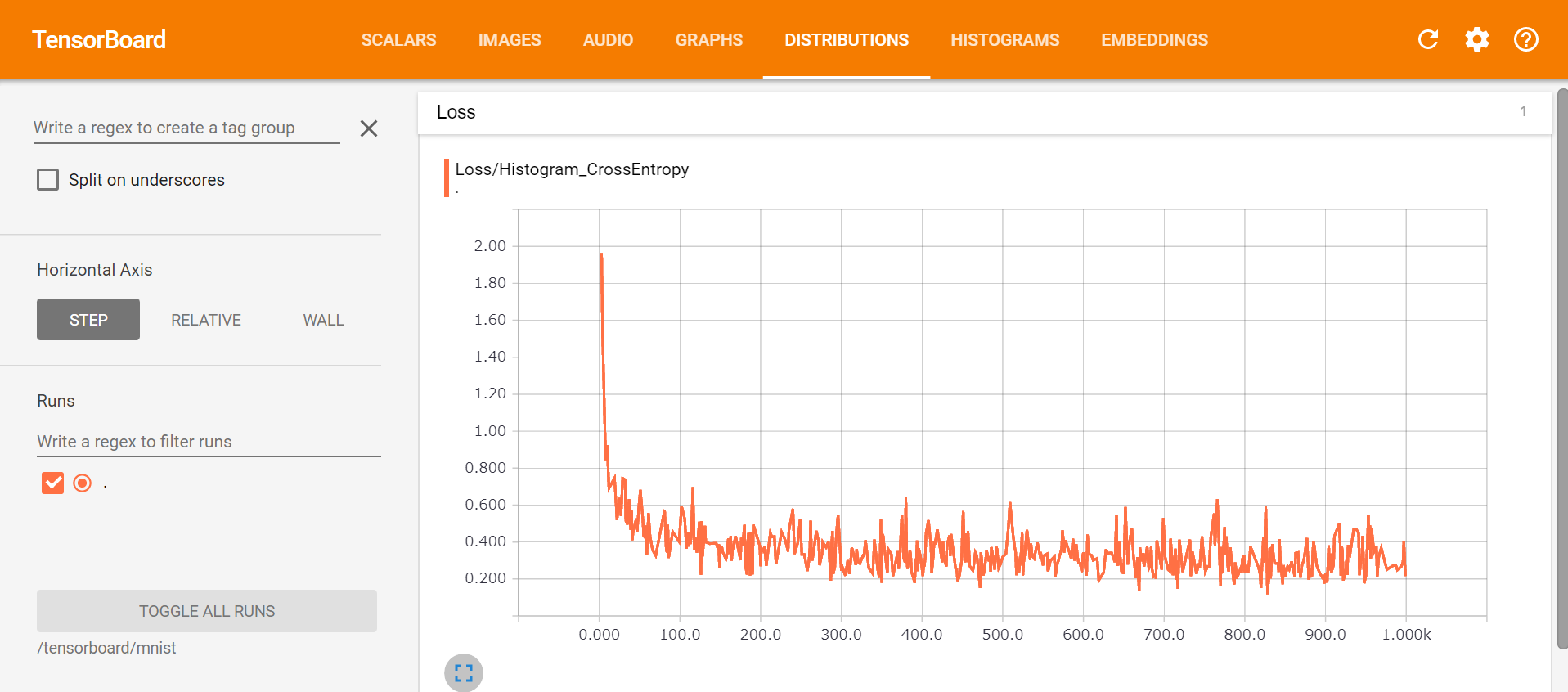
損失関数が徐々に下がっている様子が分かります。後半はほとんど下がっていないので200回くらいの学習で十分だったことがうかがえます。また、グラフ構造も以下のように可視化できました。

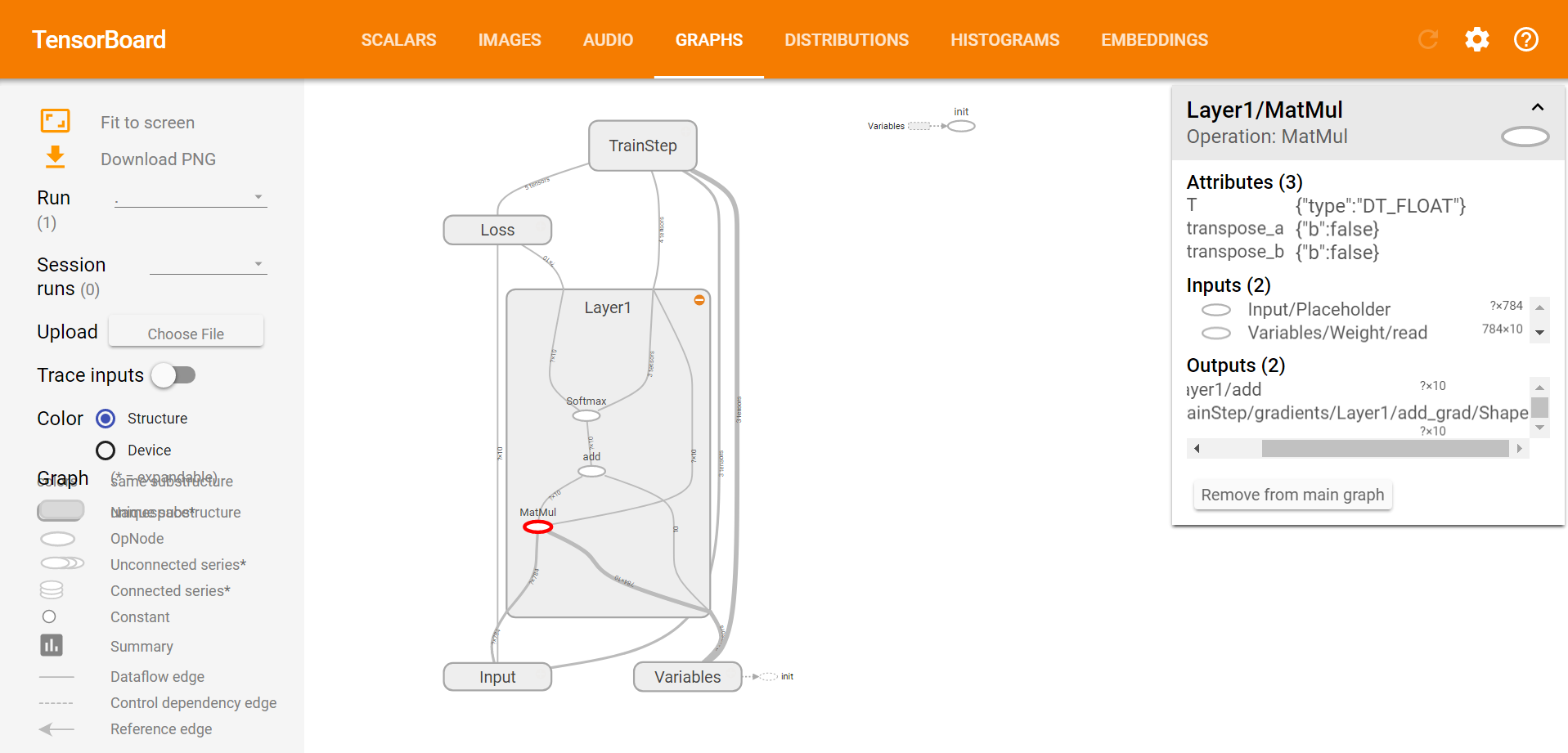
以上チュートリアルで簡単に手書き数字を認識するニューラルネットワークを実装できました。

次回はCNNの実装も紹介したいと思います。

AI・機械学習

この記事のタグ

たかはしインターン生のたかはしです。
東京大学法学部に所属しています。
プログラミング初心者なので勉強の日々です。
よろしくお願いします。