はじめに

前回のイントロでは詳しくは説明しなかった、量子コンピュータが扱うデータの最小単位であるqubitについて説明していこうと思います。

 

イントロでは、古典コンピュータが扱う通常のbitについて、電圧が高い/低い、という物理的実体を与えました。

 

しかし、qubitの物理的実体を理解するのは難しいです。そのためここでは紹介するだけにします。

現在qubitの物理的実現方法として、超伝導を使った方法がメジャーです。IBMやGoogleといった大企業がこの方法の量子コンピュータを開発しています。

 

ほかにも光を用いた量子コンピュータも研究されており、東京大学の古澤明さんがこの分野で有名です。

 

（ちなみに富士通や日立といった日本企業はイントロで軽く触れた、量子アニーリング方式を開発しています）

 

 

このようにqubitの実現には様々な方法がありますが、量子アルゴリズムを考えるうえで重要になる、qubitの性質はどれも同じです。

以下では、qubitを数学的・量子力学的な対象として説明します。

 qubitとは

「qubitとは二準位系の量子状態のことである」

 

量子力学を勉強したことがある人にとっては上の説明が最も簡潔で分かりやすいと思います。

 

。。。こんなんじゃわかんねーよ！！

って方に向けてqubitを説明するのがこの記事の目的なのでちゃんと説明します。。はい。

 

まず二準位系とは、２つの状態しかないということです。つまり

• 電圧が高い/低い
• 電流が時計回り/反時計回りに流れている
• 矢印が上/下を向いている

といったような状況だけを考える、ということです。

これだけだと、”0″と”1″という２つの古典的状態を持った古典コンピュータのbitです。

 

 

しかしこの二準位系を量子力学的にとらえると、不思議なことになります。

 

量子力学では２つの状態があった時、その２つの状態の重ね合わせの状態もある、という約束があります。

では、重ね合わせの状態とはいったいどんな状態でしょうか。

 

 

よく重ね合わせの状態は「状態”0″であり、かつ状態”1″であるような状態」と言われます。

ではそういう「状態”0″であり、かつ状態”1″であるような状態」を実際に観測してみると、本当に状態”0″で、かつ状態”1″であるような状態が得られるのでしょうか。

もちろんこの答えはNoです。

まず、そもそも矢印が上/下を向いているような状況だけを考えているので、矢印が上を向いていてさらに下を向いているという状態はありません（というかそもそも上も下も向いた矢印ってなんなんだよ…）

 

 

実は「状態”0″であり、かつ状態”1″であるような状態」を観測しても、状態”0″または状態”1″のどちらかしか得られません。

 

では、「状態”0″であり、かつ状態”1″であるような状態」と状態”0″や状態”1″との違いは何なんでしょうか。

 

その違いは、複数回観測してみると分かります。

状態”0″は何回測定しても、状態”0″である、という当然の結果だけです。状態”1″についても同じです。

しかし、「状態”0″であり、かつ状態”1″であるような状態」は全く違います。

この状態を測定すると、あるときは状態”0″であるという結果が得られ、またある時は状態”1″という結果が得られます。

しかしどちらの状態が観測されるかはランダムではありません。

ある確率Pで状態”0″が観測され、確率1−Pで状態”1″が観測されます。

 

「状態”0″であり、かつ状態”1″であるような状態」というのはこういう意味です。

 

 

したがって、量子力学では、

• 観測すると絶対に”0″/”1″が得られる状態

だけでなく、

• 観測すると確率的に”0″や”1″が得られる重ね合わせの状態

も存在します。

これらをまとめたものが量子状態です。

 

したがってqubitとは、状態”0″と状態”1″さらにその重ね合わせの状態のどれかをとるbitです。

 ディラックの記法

上で述べたことを数式で扱うには、ブラベクトル、ケットベクトルを用いたディラック記法がよく使われます。

 

２つの状態”0″, “1”を表すのにベクトルを用います。

ここで状態”0″のベクトルを表す記号を|0〉、状態”1″のベクトルを表す記号を|1〉として、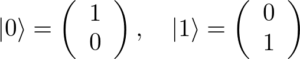

のように、２成分のベクトルを定義します。

この|0〉や|1〉をケットベクトルと言います。

すると重ね合わせの状態|ψ〉は

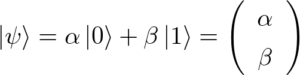
で表されます。ここでα,βは複素数です。

さらに、|α|²+|β|²=1とすると|α|²が状態|0〉が得られる確率、|β|²が状態|1〉が得られる確率を表していると解釈できます。