qubitのおさらい

qubitについての記事では、

「qubitとは二準位系の量子状態のことである」

と説明しました。

また、ディラック記法を使うと重ね合わせまで含めた二準位系の任意の量子状態|ψ〉は状態|0〉, |1〉の線形結合として

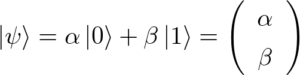
と表現されるのでした。

 qubitの可視化 —ブロッホ球—

量子コンピュータでは量子状態|ψ〉に様々な変換を施していきます。

計算の各ステップで量子状態は常に変わり続けますが、その変化を上で説明したディラック記法を用いた、式での表現で追い続けるのは簡単ではないでしょう。

また、式を追うだけでは量子計算で頻出するPauli-Z ゲートやHadamard ゲートといった量子ゲートが、量子状態|ψ〉をどのように変換するのかを直観的に理解するのは難しいでしょう。

そこで、ブロッホ(bloch)球です。

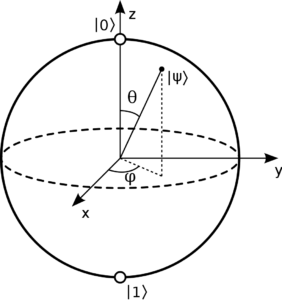
Smite-Meister [CC BY-SA 3.0], via Wikimedia Commons

状態|ψ〉が単位球面上の点として表現されている

ブロッホ球とは、qubitを球面上の１点として表現したものです。

確率の総和が１であることからブロッホ球は単位球です。

qubitを球面上の１点として理解することで、視覚的に量子状態を見ることができ、さらには計算をしなくても量子ゲートによるqubitの変換を理解することができます。

とにかく量子コンピュータを理解するうえで、ブロッホ球の考え方を知っていると便利なんです！

図を見ていただければわかる通り、z軸の上方向を状態|0〉、下方向を状態|1〉とするのが慣例です。

したがって、北極点が純粋な|0〉の状態、南極点が純粋な|1〉の状態、それ以外が|0〉, |1〉の重ね合わせの状態に対応します。

図中のθ, φはそれぞれ緯度、経度を表しています。

さらにPauli-Z ゲートやHadamard ゲートといった量子ゲートは、ブロッホ球での回転や鏡映反転に対応します。