遺伝的プログラミングで○×ゲームAI制作に挑戦！

Date:2018.02.23

まついりょう

○×ゲームAI

遺伝的プログラミング(以下GP)は機械学習の一種で、「最適な関数を求める」ことを可能とするアルゴリズムです。GPに関する基礎理論は過去の記事をご覧ください。

今回はGPのこの性質を応用し、○×ゲームの「必勝関数」を求め、それを実行する人工知能AIの制作に挑戦していきます。

以下では機械学習に適したプログラミング言語、python3によって実装していきますが、コーディング力に乏しいため、コーディングの汚さについてはご容赦ください。

1.GP基本用語

この記事で用いるGPの基本用語をあらかじめ定義しておきます。

関数：

ここでは「関数」という言葉は数学における関数のみを表すことにします。

(y=ax+bにおいて、yは関数であり、xが変数、a,bが定数です。)

演算子:

厳密な定義はなく、GPのユーザーが自由に決められますが、四則演算(y=a+b)やy=sinx,y=exp(x)などの単純な関数が主に用いられます。(過去の記事「遺伝的アルゴリズム・遺伝的プログラミング」p26 上部「簡単な関数」と同じものを指します。)

制御関数:

ここではGPを制御するためのプログラミングにおける関数を「制御関数」と呼ぶことにします。

個体：

“進化”させる対象のもの。GPにおいては主に一つの関数が一つの個体としてみなされます。

遺伝子木:

個体がy=ax+bのような関数であるとき、この式をツリー状に表したものが遺伝子木で、この遺伝子木が個体の遺伝子とみなされます。

葉：

遺伝子木を構成する点のことを指し、演算子、変数、定数の三種類の葉があります。

2.GPの実装

まずは○×ゲームに関係なく、汎用的に使用できるGPの基礎部分の実装を「集合知プログラミング(オライリー社)」を参考に、少々改良して実装していきます。

まずはモジュールのインポート。

from random import random, randint, choice
from copy import deepcopy, copy
from math import log
import numpy as np

from random import random, randint, choice

from copy import deepcopy, copy

from math import log

import numpy as np

そして演算子群を定義します。

fwrapper：演算子に名前や引数の数(childcount)の情報を付加したオブジェクト

functionbox:GPに使用する数種類のfwarpper オブジェクトをまとめるオブジェクト

class fwrapper:
    def __init__(self,function,childcount,name):
        self.function=function
        self.childcount=childcount
        self.name=name

class functionbox:
    def __init__(self):
    
        def safe_div(l):
            if l[1]!=0:
                return l[0]/l[1]
            else:
                return 0
        
        def if_func(l):
            if l[0]>l[1]:
                return 1
            else:
                return 0
        
        iff = fwrapper(if_func, 2, 'iff')   
        add = fwrapper(lambda l: l[0] + l[1], 2, 'add')
        sub = fwrapper(lambda l: l[0] - l[1], 2, 'sub')
        mul = fwrapper(lambda l: l[0] * l[1], 2, 'mul')
        maxw = fwrapper(lambda l: max(l[0], l[1]), 2, 'maxw')
        minw = fwrapper(lambda l: min(l[0], l[1]), 2, 'minw')
        iff = fwrapper(if_func, 2, 'iff')
        div = fwrapper(safe_div,2,'div')
    
        self.box=list([add,sub,mul,div,maxw,minw,iff])

    def append(self,fw):
        self.box.append(fw)
    
    def remove(self,fwname):
        if fwname in [i.name for i in self.box]:
            self.box.pop([i.name for i in self.box].index(fwname))
        else:
            print("nothing")
        
    def showbox(self):
        print([i.name for i in self.box])
    
    def funcchoice(self):
        return choice(self.box)

class fwrapper:

def __init__(self,function,childcount,name):

self.function=function

self.childcount=childcount

self.name=name

class functionbox:

def __init__(self):

def safe_div(l):

if l[1]!=0:

return l[0]/l[1]

else:

return 0

def if_func(l):

if l[0]>l[1]:

return 1

else:

return 0

iff = fwrapper(if_func, 2, 'iff')

add = fwrapper(lambda l: l[0] + l[1], 2, 'add')

sub = fwrapper(lambda l: l[0] - l[1], 2, 'sub')

mul = fwrapper(lambda l: l[0] * l[1], 2, 'mul')

maxw = fwrapper(lambda l: max(l[0], l[1]), 2, 'maxw')

minw = fwrapper(lambda l: min(l[0], l[1]), 2, 'minw')

iff = fwrapper(if_func, 2, 'iff')

div = fwrapper(safe_div,2,'div')

self.box=list([add,sub,mul,div,maxw,minw,iff])

def append(self,fw):

self.box.append(fw)

def remove(self,fwname):

if fwname in [i.name for i in self.box]:

self.box.pop([i.name for i in self.box].index(fwname))

else:

print("nothing")

def showbox(self):

print([i.name for i in self.box])

def funcchoice(self):

return choice(self.box)

funcitonboxクラスではデフォルトで四則演算、最大値などが入っているように書いてありますが、appendメソッドやremoveメソッドで自由に変更できます。

次に、葉の定義です。

node: 演算子の葉

paramnode: 変数の葉

constnode: 定数の葉

class node:
    def __init__(self, fw, children,paramlist):
        self.function = fw.function
        self.name = fw.name
        self.children = children
        self.paramlist = paramlist

    def evaluate(self, inp):
        result = [n.evaluate(inp) for n in self.children]
        return self.function(result)

    def display(self, indent=0):
        print("  " * indent + self.name)
        for c in self.children:
            c.display(indent + 1)

    def depthcount(self):
        return max([i.depthcount() for i in self.children]) + 1

    def nodecount(self):
        return sum([n.nodecount() for n in self.children]) + 1

class node:

def __init__(self, fw, children,paramlist):

self.function = fw.function

self.name = fw.name

self.children = children

self.paramlist = paramlist

def evaluate(self, inp):

result = [n.evaluate(inp) for n in self.children]

return self.function(result)

def display(self, indent=0):

print(" " * indent + self.name)

for c in self.children:

c.display(indent + 1)

def depthcount(self):

return max([i.depthcount() for i in self.children]) + 1

def nodecount(self):

return sum([n.nodecount() for n in self.children]) + 1

class paramnode:
    def __init__(self, paramname,paramlist):
        self.paramname = paramname
        self.paramlist = paramlist

    def evaluate(self, inp):
        return inp[self.paramlist.index(self.paramname)]

    def display(self, indent=0):
        print ("  " * indent, self.paramname)

    def depthcount(self):
        return 1

    def nodecount(self):
        return 1

class paramnode:

def __init__(self, paramname,paramlist):

self.paramname = paramname

self.paramlist = paramlist

def evaluate(self, inp):

return inp[self.paramlist.index(self.paramname)]

def display(self, indent=0):

print (" " * indent, self.paramname)

def depthcount(self):

return 1

def nodecount(self):

return 1

class constnode:
    def __init__(self, v,paramlist):
        self.v = v
        self.paramlist = paramlist

    def evaluate(self, inp):
        return self.v

    def display(self, indent=0):
        print ("  " * indent, self.v)

    def depthcount(self):
        return 1

    def nodecount(self):
        return 1

class constnode:

def __init__(self, v,paramlist):

self.v = v

self.paramlist = paramlist

def evaluate(self, inp):

return self.v

def display(self, indent=0):

print (" " * indent, self.v)

def depthcount(self):

return 1

def nodecount(self):

return 1

nodeはその演算子の変数の数だけ子となる葉(node,paramnode,constnodeのうちのどれか）を設定します。子にもう一度演算子の葉が設定された場合、さらにその葉にも子(はじめの葉にとっての孫)となる葉が定義され、それが再帰的に続くことでツリー状遺伝子が生成されていきます。これは、一つのオブジェクトを定義するとそのオブジェクト自体は葉一枚を表しますが、子という属性関係によってつながることで結果として遺伝子木全体を表していると言え、それら演算子、変数、定数の組み合わせが関数として成り立ちます。

この三つのクラスすべての初期化(制御)関数の引数にあるparamlistは変数の名前が入れられたリストで、paramnodeにはこのうちのどれかが割り当てられます。paramlistの対応する位置に変数の値を入れたリストを与えると、その変数値の情報を取得します。

node,paramnode,constnodeはメソッドの名前も共通しています。evaluateは上記のように遺伝子木に変数を与え、値を出力させるメソッド、displayは関数を表示するメソッド、depthcountは葉がどれだけの深さであるかをカウントするメソッドです。これらのメソッドは木全体に行う操作の一部分を表しますが、上記のように葉どうしに親子関係があることで、子の葉のメソッドの結果を受け取り、集計して親に返すことが可能となり、最終的に木全体の結果が得られる仕組みになっています。(今回はこの3つのメソッドのみ使用します。)

次にGPの制御関数を定義します。

まずは遺伝子木をランダムに生成する制御関数(makerandomtree)です。

def makerandomtree(fb, paramlist, fpr, ppr, maxdepth):
    if random() < fpr and maxdepth > 0:
        f = fb.funcchoice()
        children = [makerandomtree(fb,paramlist,fpr,ppr,maxdepth=maxdepth-1) for i in range(f.childcount)]
        return node(f, children,paramlist)

    elif random() < ppr:
        return paramnode(choice(paramlist),paramlist)

    else:
        return constnode(randint(1, 20) - 10,paramlist)

def makerandomtree(fb, paramlist, fpr, ppr, maxdepth):

if random() < fpr and maxdepth > 0:

f = fb.funcchoice()

children = [makerandomtree(fb,paramlist,fpr,ppr,maxdepth=maxdepth-1) for i in range(f.childcount)]

return node(f, children,paramlist)

elif random() < ppr:

return paramnode(choice(paramlist),paramlist)

else:

return constnode(randint(1, 20) - 10,paramlist)

引数はfbがfunctionboxオブジェクト、paramlistが前述通り変数の名称リスト、fprが演算子の葉の生成確率、pprが演算子の葉と変数の葉の生成確率の和(ppr-fprが変数の葉の生成確率,1-fprが定数の葉の生成確率)、maxdepthが遺伝子木の深さ制限、です。

これも前述の再帰構造を用いていますが、この制御関数によって具体的な遺伝子木が生成されることになります。

さらに、遺伝操作を制御する制御関数を定義します。

cross：交叉

mutate：突然変異

def cross(t1, t2, probswap):
    if random() < probswap :
        return deepcopy(t2)

    else:
        result = deepcopy(t1)
        if hasattr(t1, 'children') and hasattr(t2, 'children'):
            if len(result.children) == 1:
                r = 0
            else:
                r = randint(0, len(result.children) - 1)
            result.children[r] = cross(t1.children[r], choice(t2.children),probswap)
        return result

def cross(t1, t2, probswap):

if random() < probswap :

return deepcopy(t2)

else:

result = deepcopy(t1)

if hasattr(t1, 'children') and hasattr(t2, 'children'):

if len(result.children) == 1:

r = 0

else:

r = randint(0, len(result.children) - 1)

result.children[r] = cross(t1.children[r], choice(t2.children),probswap)

return result

def mutate(t, probchange,fb, paramlist, fpr, ppr):
    if random() < probchange:
        return makerandomtree(fb, paramlist, fpr, ppr,maxdepth=t.depthcount())
    else:
        result = deepcopy(t)
        if hasattr(t, "children"):
            if len(result.children) == 1:
                r = 0
            else:
                r = randint(0, len(result.children) - 1)
            result.children[r] = mutate(t.children[r], probchange,fb, paramlist, fpr, ppr)
        return result

def mutate(t, probchange,fb, paramlist, fpr, ppr):

if random() < probchange:

return makerandomtree(fb, paramlist, fpr, ppr,maxdepth=t.depthcount())

else:

result = deepcopy(t)

if hasattr(t, "children"):

if len(result.children) == 1:

r = 0

else:

r = randint(0, len(result.children) - 1)

result.children[r] = mutate(t.children[r], probchange,fb, paramlist, fpr, ppr)

return result

crossは個体t1の一部分を個体t2の一部分と同じものに置き換える「交叉」、mutateは個体tのある一部分を新たにランダムに作り直す「突然変異」を制御する制御関数です。

crossの引数は二つの個体t1,t2とprobswapで、probswapはある葉を交叉点として選ぶ確率、1-probswapがそれよりも下にある葉を交叉点として選ぶ確率です。そのため、制御関数crossはまず初めに個体t1の頂点に対して、交叉点とするかどうかを決め、選ばれた場合個体t2を返します。(交叉点が頂点ならt1の入れ替える部分はt1の全体に一致するから。)選ばれなければランダムに一つ頂点の子の葉を選択し、その葉に同様な操作を行います。これを繰り返すことで遺伝子木のどこかの点を交叉点として指定する子ができます。指定ができたら、その点より下の部分をt2の一部分と同じものに置き換えます。また、ある葉が交叉点として選ばれず、子に受けわたったとき、置き換えるt2の交叉点もランダムに子に受け渡すことで遺伝子木の深さを一定にし、深さの爆発を防いでいます。

また、mutateの引数は個体tとprobchangeで、これもcrossと同じく、ある葉を突然変異の開始点として選ぶ確率です。そのためcrossと同様に頂点から選ぶか選ばないかを繰り返して、子に受け渡していき、選択された点より下の構造を新しい遺伝子木に付け替えます。ここで新しく作る遺伝子木は上記のmakerandomtreeを用いますが、子に受け渡すたびに深さ制限を引き下げていくことでこちらも深さの爆発を防ぎます。

次は評価値の順に個体を並べなおす制御関数(rankfunction)です。

def rankfunction(population,scorefunction,paramlist):
    scores = scorefunction(population,paramlist)
    sortedscores = sorted(scores, key=lambda x: x[0],reverse=True)
    return sortedscores

def rankfunction(population,scorefunction,paramlist):

scores = scorefunction(population,paramlist)

sortedscores = sorted(scores, key=lambda x: x[0],reverse=True)

return sortedscores

この引数は、populationが並べなおす前の個体群、scorefunctionが評価値を計算させる制御関数、pramlistはnodeオブジェクトなどと同様に変数名リスト、です。scorefunctionについてはユーザーが用途によって変更できるもので、個体群populationとparamlistを引数に[[評価値1,個体1],[評価値2,個体2],…,[評価値n,個体n]]のような形になるリストを返す制御関数です。今回は○×ゲームの勝敗数から評価値を計算したいので、○×ゲームの実装後に設定します。

また、scorefunctionによって得られた二次元リストを評価値をキーとしてソートしたものを返すことで目的を果たします。

最後にメインとなる、個体を進化させる制御関数(evolve)です。

def evolve(maxgen,popsize,fb,paramlist,scorefuncion,maxdepth,fpr,ppr,pnew,pexp,probswap,probchange):
    def selectindex():
        return min(popsize - 1, int(log(random()) / log(pexp)))

    population = [makerandomtree(fb,paramlist,fpr,ppr,maxdepth) for i in range(popsize)]
    for i in range(maxgen):
        scores = rankfunction(population,scorefuncion,paramlist)
        print ("{}:{}".format(i, scores[0][0]))
        newpop = [scores[0][1], scores[1][1]]

        while len(newpop) < popsize:
            if random() > pnew:
                newpop.append(mutate(cross(scores[selectindex()][1],scores[selectindex()][1],probswap),
                                     probchange,fb, paramlist, fpr, ppr))
            else:
                newpop.append(makerandomtree(fb,paramlist,fpr,ppr,maxdepth))

        population = newpop

    scores[0][1].display()

    return scores[0][1]

def evolve(maxgen,popsize,fb,paramlist,scorefuncion,maxdepth,fpr,ppr,pnew,pexp,probswap,probchange):

def selectindex():

return min(popsize - 1, int(log(random()) / log(pexp)))

population = [makerandomtree(fb,paramlist,fpr,ppr,maxdepth) for i in range(popsize)]

for i in range(maxgen):

scores = rankfunction(population,scorefuncion,paramlist)

print ("{}:{}".format(i, scores[0][0]))

newpop = [scores[0][1], scores[1][1]]

while len(newpop) < popsize:

if random() > pnew:

newpop.append(mutate(cross(scores[selectindex()][1],scores[selectindex()][1],probswap),

probchange,fb, paramlist, fpr, ppr))

else:

newpop.append(makerandomtree(fb,paramlist,fpr,ppr,maxdepth))

population = newpop

scores[0][1].display()

return scores[0][1]

この引数は、maxgenが最終世代(最適解を決定する世代)、popsizeが一世代あたりの個体の数、pnewが新世代の中に前の世代に影響されていない全く新しい個体を生み出す確率、pexpが多様性の優先度合い(高いほど多様性重視)で、そのほかはこれまで記述したものと同じです。

まず初めに多様性の優先度合いを考慮する制御関数selectindexを設定します。これは多様性の優先度合いが低いほど、0に近い値を返しやすくなるもので、0からpopsize-1の整数が返ってきます。これをインデックスとしてひょうリストからランダムな抽出を繰り返すことで”淘汰”をすることができます。(while文でpopsizeになるまで抽出を繰り返している)

その次からの主な流れは、前記事通り、進化(交叉、突然変異)→集団の評価→淘汰→進化→評価→淘汰→・・・→淘汰→最適解選出、になります。ここに関してはほとんどあらかじめ作成ておいた制御関数を並べているだけですが、これによって進化が完了します。

以上のプログラムを使えば評価値の設定をするだけでGPを動かすことができます。〇×ゲームでないゲームやゲーム以外のものにも様々使い道があると思うので、もし良ければ使ってみてください。

3.遺伝子木で〇×ゲーム

次に、関数から○×ゲームを対戦させる個体を設定する必要があります。

○×ゲームにおいて、何から判断して行動を決定するかというと、それは盤面にほかなりません。

よって、盤面の情報を入力として、どこに〇(または×)を置くべきかという出力ができる関数が必要です。

そこで9マスそれぞれの状態を変数に持つ9変数関数から0~8の9つの整数のうちのどれかを出力する関数を作ればよいと考えられます。

これを考慮するために、次のような設定します。

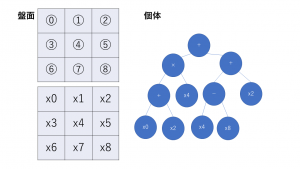
盤面の設定：

・9マスそれぞれに0~8の番号を振る

・i番のマスに〇(×)が置いてあればxi=1(2)、何も置いてなければxi=０とする。(i=0,1,2…8)

個体の設定：

1.それらx0~x8を変数として個体に読み込ませ、出力を得る。

2.その出力に0~8の整数という制約をかけるのは難しいので、出力に対して9で割ったあまりをｙとする。

3.ｙ番目のマスに〇(×)を置く。

4.ただし、y番目のマスが空いてなければy=(y+1)%9 として3.に戻る。(a%b はaをbで割ったときのあまり)

これによって個体を9変数関数として設定でき、その出力をゲームの行動に変換できます。

4. ○×ゲームの実装

上記の設定を実装し、個体同士が○×ゲームを対戦するプログラムを作成していきます。

まず、盤面を図で表示するために作図のモジュールmatplotlibをimportします。

import matplotlib.pyplot as plt

1	import matplotlib.pyplot as plt

それができたら盤面を表示する制御関数(design)を作っていきます。

def design(field):
    ax = plt.axes([0.025,0.025,0.95,0.95])
    ax.text(0.3,3.2,"赤：先行",fontsize = 20,color="red")
    ax.text(2.3,3.2,"青: 後攻",fontsize = 20,color ="blue")
    ax.text(1,-0.5,"○×ゲーム",fontsize =30,fontweight = "bold")
    ax.set_xlim(0,3)
    ax.set_ylim(0,3)
    ax.xaxis.set_major_locator(plt.MultipleLocator(1.0))
    ax.yaxis.set_major_locator(plt.MultipleLocator(1.0))
    ax.grid(which='major', axis='x', linewidth=0.75, linestyle='-', color='0')
    ax.grid(which='major', axis='y', linewidth=0.75, linestyle='-', color='0')
    ax.set_xticklabels([])
    ax.set_yticklabels([])
    for i,a in enumerate(field):
        if a == 1:
            col = "red"
            circle = plt.Circle(((i%3+1)-0.5,(3-i//3)-0.5),0.4,color = col)
            ax.add_patch(circle)
        elif a == 2:
            col = "blue"
            circle = plt.Circle(((i%3+1)-0.5,(3-i//3)-0.5),0.4,color = col)
            ax.add_patch(circle)
    plt.show()

def design(field):

ax = plt.axes([0.025,0.025,0.95,0.95])

ax.text(0.3,3.2,"赤：先行",fontsize = 20,color="red")

ax.text(2.3,3.2,"青: 後攻",fontsize = 20,color ="blue")

ax.text(1,-0.5,"○×ゲーム",fontsize =30,fontweight = "bold")

ax.set_xlim(0,3)

ax.set_ylim(0,3)

ax.xaxis.set_major_locator(plt.MultipleLocator(1.0))

ax.yaxis.set_major_locator(plt.MultipleLocator(1.0))

ax.grid(which='major', axis='x', linewidth=0.75, linestyle='-', color='0')

ax.grid(which='major', axis='y', linewidth=0.75, linestyle='-', color='0')

ax.set_xticklabels([])

ax.set_yticklabels([])

for i,a in enumerate(field):

if a == 1:

col = "red"

circle = plt.Circle(((i%3+1)-0.5,(3-i//3)-0.5),0.4,color = col)

ax.add_patch(circle)

elif a == 2:

col = "blue"

circle = plt.Circle(((i%3+1)-0.5,(3-i//3)-0.5),0.4,color = col)

ax.add_patch(circle)

plt.show()

*matplotlibで”赤：先行”のように日本語を使うには別途、設定が必要です。

次に、これを使って対戦するためのクラス(OXgame)

import numpy as np

class OXgame:
    def __init__(self,p1,p2,pramlist):
        self.field = np.zeros(9)
        self.ps = [p1,p2]
        self.params = pramlist
        
    def win_judge(self,p):
        judge = np.zeros(7)
        patterns = [(0,1,2),(3,4,5),(6,7,8),(0,3,6),(1,4,7),(2,5,8),(0,4,8),(2,4,6)]
        for pat in patterns:
            if self.field[pat[0]] == self.field[pat[1]] == self.field[pat[2]] == p:
                return p
        return False
    
    def set_judge(self,x):
        return self.field[int(x)] != 0
    
    def turn(self,p,x):
        self.field[int(x)] = p
        
    def GPgame(self):
        win = 0
        for i in range(9):
            p = self.ps[i%2]
            point = p.evaluate(self.field,self.params)%9
            if self.set_judge(point):
                while self.set_judge(point) == True:
                    point = (point+1)%9
            self.turn(i%2+1,point)
            if self.win_judge(i%2+1) == i%2+1:
                win = i%2+1
                break
        return win
    
    def Human_CPUGame(self,point,order=1):
        if order == 2 and np.all(self.field== 0):
             self.turn(1,p1.evaluate(self.field,self.params)%9)
        
        else:
            if self.set_judge(point):
                while self.set_judge(point) == True:
                    point = (point+1)%9
        
            self.turn(order,point)
            if self.win_judge(order) == order:
                print("player wins the game")
                
            else:
                point = p1.evaluate(self.field,self.params)%9
                if self.set_judge(point):
                    while self.set_judge(point) == True:
                        point = (point+1)%9
                    
                self.turn(order%2+1,point)
                if self.win_judge(order%2+1) == order%2+1:
                    print("CPU wins the game")
        
        print(np.reshape(self.field,[3,3]))

import numpy as np

class OXgame:

def __init__(self,p1,p2,pramlist):

self.field = np.zeros(9)

self.ps = [p1,p2]

self.params = pramlist

def win_judge(self,p):

judge = np.zeros(7)

patterns = [(0,1,2),(3,4,5),(6,7,8),(0,3,6),(1,4,7),(2,5,8),(0,4,8),(2,4,6)]

for pat in patterns:

if self.field[pat[0]] == self.field[pat[1]] == self.field[pat[2]] == p:

return p

return False

def set_judge(self,x):

return self.field[int(x)] != 0

def turn(self,p,x):

self.field[int(x)] = p

def GPgame(self):

win = 0

for i in range(9):

p = self.ps[i%2]

point = p.evaluate(self.field,self.params)%9

if self.set_judge(point):

while self.set_judge(point) == True:

point = (point+1)%9

self.turn(i%2+1,point)

if self.win_judge(i%2+1) == i%2+1:

win = i%2+1

break

return win

def Human_CPUGame(self,point,order=1):

if order == 2 and np.all(self.field== 0):

self.turn(1,p1.evaluate(self.field,self.params)%9)

else:

if self.set_judge(point):

while self.set_judge(point) == True:

point = (point+1)%9

self.turn(order,point)

if self.win_judge(order) == order:

print("player wins the game")

else:

point = p1.evaluate(self.field,self.params)%9

if self.set_judge(point):

while self.set_judge(point) == True:

point = (point+1)%9

self.turn(order%2+1,point)

if self.win_judge(order%2+1) == order%2+1:

print("CPU wins the game")

print(np.reshape(self.field,[3,3]))

今回はGPの実装をメインとしているため、○×ゲームの実装についての説明は省略します。

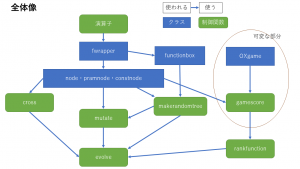
また、今回のプログラムの全体像は下のようになります。可変な部分を調整することでGPを様々な場面で使用することができます。

5. 評価値算出

GPにおいて、評価値を算出する手法として大きく絶対評価と相対評価に分けられます。

絶対評価はある個体の評価が一意に定まるため、直観的にもより安定的な解が得られると考えられます。しかし、これには客観評価が必要なため、教師データなどの独立な数値基準が必要となります。ただ、今回は○×ゲームを学習させるため、その教師データを集めるには、人間と対戦してその勝敗情報を逐一取らなくてはなりません。もちろん、GPにおいては膨大な数のランダム抽出による近似解を求める方法ですので、その対戦も膨大な数必要となり、これは効率的でありません。そこで、人間が最善手を打って学習させることを断念し、個体同士に何度も対戦させ合い、その中で強かったものに高い評価を与えるという方法をとることでこの問題を解決します。これが相対評価です。

そこで今回は以下のような設定をして評価値を算出しました。

・ある個体群に対して先行、後攻の２パターンで総当たりをし、勝3点、分け1点、負け0点して最終結果を評価値とする。

以上の内容を実装した評価値算出の制御関数は以下になります。

def gamescore(population,paramlist):
    score = np.zeros(len(population))
    for i,pi in enumerate(population):
        for j,pj in enumerate(population):
            if i == j: continue
            OX = OXgame(pi,pj,paramlist)
            win =  OX.GPgame()
            if win == 1:
                score[i] += 3
            elif win == 2:
                score[j] += 3
            else:
                score[i]+=1
                score[j]+=1
    scores = [[score[i],t] for i,t in enumerate(population)]
    return scores

def gamescore(population,paramlist):

score = np.zeros(len(population))

for i,pi in enumerate(population):

for j,pj in enumerate(population):

if i == j: continue

OX = OXgame(pi,pj,paramlist)

win = OX.GPgame()

if win == 1:

score[i] += 3

elif win == 2:

score[j] += 3

else:

score[i]+=1

score[j]+=1

scores = [[score[i],t] for i,t in enumerate(population)]

return scores

前述通り。引数には個体群populationと変数名リストparamlistが入ります。

まず得点を記述するための配列scoreを用意して、for文のに二重ループで総当たりしていきます。iが先行、jが後攻としているため、これによって先行、後攻をいれかえたパターンでも総当たりができています。

全対戦終了後、スコアと個体を紐づけして返せば、GPのscorefunctionの役割を果たせます。

6. 結果

以上を実行します。

fb=functionbox()
paramlist = ["x0","x1","x2","x3","x4","x5","x6","x7","x8"]
CPU = evolve(50,50,fb,paramlist,gamescore,10,0.75,0.9,0.2,0.7,0.5,0.5)

fb=functionbox()

paramlist = ["x0","x1","x2","x3","x4","x5","x6","x7","x8"]

CPU = evolve(50,50,fb,paramlist,gamescore,10,0.75,0.9,0.2,0.7,0.5,0.5)

まず、必要なfuncionboxとparamlistを定義して、諸パラメータ、評価値算出の制御関数などと一緒にevolveの引数に与えます。

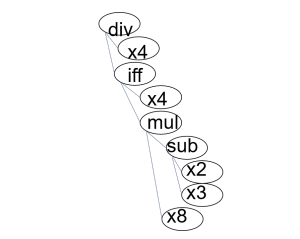
そして、出力(の一部)が以下となります。

div

iff

mul

sub

これは(printの)出力のほんの一部分で、このような遺伝子木を描いてくれます。

これは下のように読み取ることができますが、これを見ても何もわからないので、このプログラムと対戦していきます。

ちなみに、○×ゲームはお互いに最善手を打つと引き分けになります。しかし、後攻が悪手を打つと必ず勝てるパターンが存在しています。基本的に人間は考えて最善手を打てるので、目標は、後攻なら引き分け、先行なら後攻の悪手に対応して勝つことです。(先行が最善手を打ったら引き分けでよい)

それでは対戦していきます。

まずは人間先行。

1ターン目:僕(赤)が先に打って、そのあとAI(青)が打ってきます。

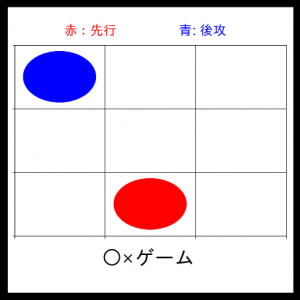
とりあえず甘い手を打ってみましたが、それなりにいい手を返してきます。

2ターン目：ところが、リーチを作ってみると、

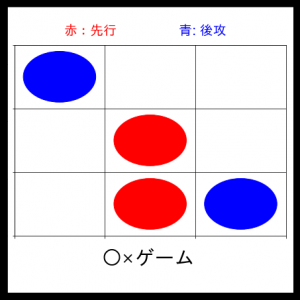
リーチを防いでくれません。

3ターン目：

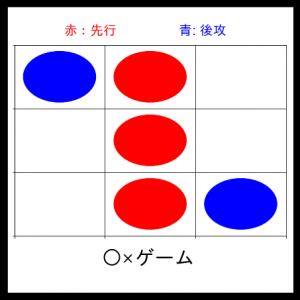
もちろんこれで僕の勝利です。

AIは後攻に弱いということも考えられますので、先攻後攻を入れ替えて検証してみます。

1ターン目：まずAI(赤)が打ってきます。

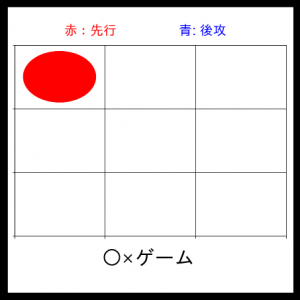
2ターン目：次からは僕(青)が打って、そのあとAIが打ち返してきます。

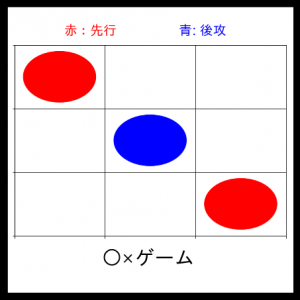
案の定あまりいい手は打ってきません。笑

3ターン目：リーチをかけてみます。

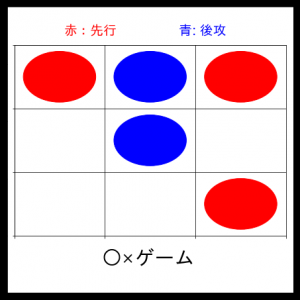
またもや僕のリーチを防げませんでした。

4ターン目：

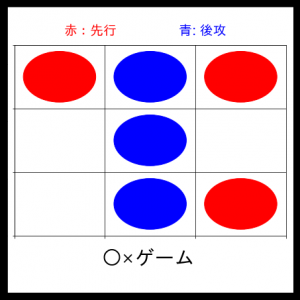
またまたこれで僕の勝利です。

結果：必勝AIは作れず。。

7. 考察

なぜ必勝AIが作れなかったのかを考察していこうと思います。

ここで挙げられる問題点はいくつかあります。

変数が多いこと。
「おける場所の中での最善」をえらんでいないこと
変数の値の大小が影響していること。

などです。

上から順に説明していきます。

そもそもGPはランダムに演算子、変数、定数を組み合わせて遺伝子木を作り出しているので、その中から最善なものを見つける場合、変数の数は少ないに越したことはありません。単純な一変数であっても様々な遺伝子木が存在するため、そこからさらに変数を増やしてしまうと組み合わせ爆発によって、解の発見がより難しくなります。

さらに、今回は置けるか置けないかを関数に判断せず、置けないマスを選んでしまったときは隣のマスに置く、という操作をしています。そのため、ターンが進んで盤面に入れられている〇×が多くなると、関数で算出した最適なマスとは異なるマスに〇や×を置いてしまうことが多くなります。これが学習において関数値の良し悪しの測定を攪乱させてしまい、うまく学習できなかったのかもしれません。

また、変数の内容についてですが、変数で何か物事の状態を表す時、一般的に「ダミー変数」と呼ばれる変数を用います。これは1,または0をとる変数であって、いわば論理型です。これは真か偽の二つの状態を表すもので、その値の大小は関係なく、「ある」か「ない」かを明確に分けられるものです。しかし、今回は簡単のため、マスの状態を0,1,2であらわしてしまいました。こうしてしまうと、計算の中に2という数字が表れることになりますが、機械はそれがマスの状態を表す変数だとは理解してくれず、「1の倍の数」として扱ってしまいます。これでは1と2という値が対をなしているという情報を与えることができていません。この偏った情報を与えてしまったことによって、うまくいかなかったとも考えられます。

この改善策としては、マスの情報を二つのダミー変数であらわすことが考えられます。一つ目が「〇が入っているか入ってないか」、二つ目が「×が入っているか入ってないか」とすることで、すべての状態を等価な情報として与えられます。しかし、このようにしてしまうと、変数の数が二倍になってしまうという問題もあります。例えば1番目のマスに〇が入っている状態を表すにはx1=1,y1=0となったり、2番目のマスに何も入ってない状態を表すにはx2=0,y2=0のように、一つのマスに対して、x,yという二つの変数が必要になってきます。このように、複数の状態を等価な情報として与えるには変数が多く必要になりますが、一方で、変数が多すぎると解の発見が難しくなるというジレンマをかかえます。

以上のように、何でもかんでも適当にGPを組むだけではうまく学習できないません。残念ながら、今回はうまくいった結果をお見せ出来ませんでしたが、多少は機械学習の難しさを理解していただけたかと思います。この記事では勝手ながらこの考察までで終わらせていただこうと思いますが、これからも上のような問題点を考察し改良を繰り返すことによって、より良いAIを作っていけたらと思います。

最後までご覧いただきありがとうございました。

AI・機械学習

この記事のタグ

まついりょう東京工業大学工学院経営工学系学士課程4年。
専門は機械学習とオペレーションズリサーチ。
最近は解釈可能機械学習とトークンエコノミーに興味があります。