テキスト自動要約サイトを公開したのでご紹介します

はじめに
この度、インターン生の活動として製作したテキスト自動要約サイトを公開しました!以下のURLからお試し頂けます。
https://labo.ef-4.co.jp/sample_products/text_sum/
ニュース記事や紹介記事などの文章を入力して、要約の制限を選択すると自動で要約してくれるツールです。
本記事ではこのアルゴリズムが内部でどのようなことをしているのかをご紹介したいと思います!
アルゴリズムの主な流れ
1. 入力された文章を句読点で一文ごとに分け、更に文を形態素解析して単語ごとに分割する。
2. 形態素解析された文をWord2Vecを用いて一文ずつベクトルに変換する。
3. 全ての2文の組み合わせに対して、Cos類似度を計算する。
4. 全ての文に対してLexRankスコアを算出する。
5. スコアが高い順に、要約の制限に達するまで文を選択する。
それぞれの行程で使われている技術について大まかに説明していきます。
1. 形態素解析
「形態素」とは、文章を構成する要素のうち、意味を持つ最小の単位のことで、多くの場合は単語に一致します。形態素解析は文章を形態素ごとに分割する作業のことをいいます。
例えば、
「I love machine learning.」
という文を形態素解析すると、
「I / love / machine / learning / .」
と分割されます。
英語の文章なら多くの場合、上記のようにスペースで分割すれば事足りますが、日本語の文章の場合そう単純ではありません。
「お待ちしております。」
という文を形態素解析すると、
「お待ち/し/て/おり/ます/。」
となります。
日本語は単語間に空白がなく単純には分けられないため、品詞の繋がり方などを考慮して単語を決定しなければならず難易度が高い言語のひとつです。自然言語処理用の辞書(コーパス)や、文法の性質などを利用して決定しますが、それでも文法だけで言えば正しいといえる分け方は複数存在してしまいます。
現在無償で入手可能な日本語の形態素解析エンジンはいくつか存在しており、今回はMeCab(http://taku910.github.io/mecab/)を用いています。
2. Word2Vec
Word2Vecは「Word to Vector」の略で、その名の通り「単語をベクトル化する手法」のことです。
これがどういうことかというと、そもそも従来の単語ベクトル表現においては、全ての単語それぞれにラベル付けをしてベクトルを表していました。
つまり1万語の単語があったら1万次元のベクトルを用いて、要素を単語に割り当てるということです。
しかしこれでは「猫」と「ねこ」と「ネコ」がすべて異なる単語として認識されることになり、表現の違いに弱くなってしまいます。
また長い文章を扱う際に非常に高次元なベクトルとなり、扱いにくいという問題点があります。
そこでWord2Vecという単語の分散表現が生まれました。これはそれぞれの単語に関わりがある要素を200次元程度のベクトル空間で表現することで、文同士のみだけでなく単語同士の演算を可能にしたものです。
ここではベクトルの要素一つ一つが、ある抽象的な意味や概念を表しています。
例えばWord2Vecが可能とする単語同士の演算の中で有名な例としては以下の式があります。
「王様」ー「男」+「女」=「女王」
この式を見ると、「王様」と「女王」の関係性は「男」か「女」かの違いであることを理解できていることがわかります。
つまりコンピュータに「意味」を理解しているような挙動をさせることが可能になります。
ではこの分散表現はどうやって取得するのかというと、大雑把に言えば「同じ文脈の中に存在する単語は近い意味を持っている」という考えに基づいてそれぞれの単語にベクトルを付与しています。これは「Skip-Gram」というニューラルネットワークモデルを用いて学習できるのですが、長くなるのでここでは具体的な説明は割愛します。
今回はWikipediaからダウンロードした大量の記事を用いて学習させたモデルを用いました。
3. Cos類似度
Cos類似度は、ある2文がベクトル空間上でどれだけ類似しているかを表す値です。x,yをそれぞれベクトルで表現された文とすると、二文のCos類似度は次のような簡単な式で求まります。
![]()
この式はベクトル同士が成す角度のコサイン値なので、値が1に近いほど2文が類似しており、0に近いほど類似していない、ということを表しています。
4. LexRank
LexRankとは文間の類似度を用いて、それぞれの文の重要度を算出するアルゴリズムです。
大まかに言うと以下のルールに基づいて重要度を決定しています。
・重要な文に類似している文は重要である
・多くの文に類似している文は重要である
ここでグラフ理論を用います。グラフとは、「点とそれらを結ぶ線の集合」という概念のことで、様々なもの同士の関連を表すことができます。
下図における数字一つ一つを頂点(またはノード)、それらを結ぶ線を辺(またはエッジ)と呼びます。
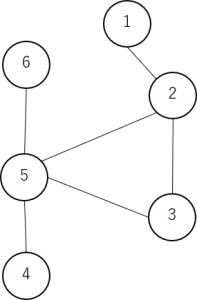
上図の場合は、1は2に関連しており、3は2と5に関連しており、5は2,3,4,6に関連している、といった関係性を表現しています。
このグラフを定量的に表す手段のひとつに「隣接行列」があります。
隣接行列は、ある頂点xとyの間に辺が存在するときには行列の(x,y)成分を1とし、存在しないときには0としたものです。
例えばこのグラフの隣接行列は以下の行列で表されます。
![Rendered by QuickLaTeX.com \[ \left( \begin{array}{cccccc} 0&1&0&0&0&0\\ 1&0&1&0&1&0\\ 0&1&0&0&1&0\\ 0&0&0&0&1&0\\ 0&1&1&1&0&1\\ 0&0&0&0&1&0 \end{array} \right) \]](/wp/wp-content/ql-cache/quicklatex.com-9f03bb3fd630ea93921f45cc9337358a_l3.png)
LexRankでは、グラフ表現における頂点を文、辺を文同士の類似度とします。
ただしCos類似度を用いて求めた類似度は0から1の間の値を取るため、類似度が閾値t以上の時は文同士を辺で結び、閾値t以下の時は結ばない、として隣接行列を作成します。
そうして求められた隣接行列を、各列の要素の和が1になるように調整して確率行列に変換します。
そしてここで、この確率行列をもとにマルコフ連鎖の定常分布を求めます。
定常分布とは、「一度その状態に入ったらずっとその状態であり続ける」ような分布のことです。
マルコフ連鎖は必ず収束することが一般に知られているため、べき乗法で転置行列を乗算していきます。
ある程度収束した時点での固有ベクトルがLexRankスコアになります。
最後にLexRankスコアの高い文から要約の制限に達するまで文を選択したら要約完了です!
おわりに
今回はLexRankというアルゴリズムを用いて文章を要約するツールを作ってみました。
ただしこの要約はあくまで「元の文章から重要そうな文を抽出しているだけ」でしかなく、人手による要約にはまだまだほど遠いものです。人間が文章を要約する際には、「文の短縮」や「文の結合」、「言い換え表現」など色々な操作を行いながら要約しています。
これらの技術をプログラムで実現するためには、コンピュータが文章の「意味」を理解できるようになる必要があり、今の時点では非常に難しいと言われています。
ただ今回作ったツールでも、少し長めのニュース記事を全て読みたくない!なんとなく重要なところだけ読みたい!というような需要には答えられるのではと思うので、是非試してみてください!
自然言語処理について勉強中です。
女子校出身のノリがキツいと周りから距離をおかれつつあります。





